| 1. Предел суммы, разности,
произведения и частного последовательностей Вычислению
пределов последовательностей помогают следующие простые свойства. |
|
1.
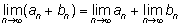
2.
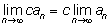
3.
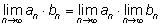
4.
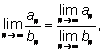 если
если
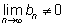
|
| Во всех этих равенствах предполагается, что все
написанные пределы существуют, или, как говорят математики, все
последовательности являются сходящимися. |
Вычислим несколько пределов с помощью сформулированных
свойств.
1.
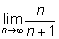
Можно поступить так:
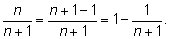
Будем считать число
1
общим членом «постоянной» последовательности, предел которой,
конечно, равен
1:
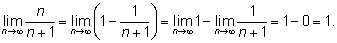
Итак,
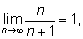 что мы, разумеется, знали и раньше
что мы, разумеется, знали и раньше
(например, когда проводили
горизонтальную асимптоту для построения графика функции
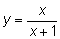 ). ).
Можно было поступить по-другому:
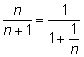 и теперь воспользоваться свойством пределов:
и теперь воспользоваться свойством пределов:
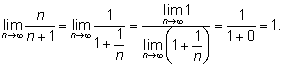
2.
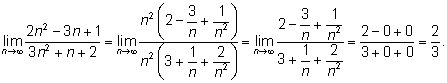
|
|
2. Признаки сходимости последовательностей.
Переход к пределам в неравенствах
Для доказательства сходимости последовательности часто полезны
следующие признаки.
|
|
Признак сходимости последовательности. Если последовательность монотонна и ограничена, то
она имеет предел. |
|
Этот признак легко иллюстрируется с помощью
числовой оси: двигаясь по ней в одну сторону и не имея возможности
перейти через поставленный барьер, мы неограниченно приблизимся к
некоторой точке числовой оси. |
В примере с корнями
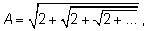 где
где
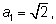 а каждый следующий член последовательности вычисляется
по рекуррентной формуле
а каждый следующий член последовательности вычисляется
по рекуррентной формуле 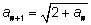 или
или
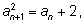 последовательность
(an)
возрастающая и ограниченная. Действительно, сначала проверим, что
an
< 2 при всех
n.
Применим индукцию:
последовательность
(an)
возрастающая и ограниченная. Действительно, сначала проверим, что
an
< 2 при всех
n.
Применим индукцию:
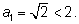 Если
an <
2,
то
an +
2 < 4 и
Если
an <
2,
то
an +
2 < 4 и
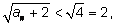 что и утверждалось. Теперь докажем возрастание последовательности.
Нам надо доказать, что
что и утверждалось. Теперь докажем возрастание последовательности.
Нам надо доказать, что
 больше, чем
an,
т. е. проверить неравенство
больше, чем
an,
т. е. проверить неравенство
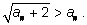 Так как
an >
0,
то его можно возвести в квадрат и получить для проверки
неравенство
Так как
an >
0,
то его можно возвести в квадрат и получить для проверки
неравенство
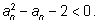 Решая неравенство
x2
– x – 2 < 0, получим промежуток
(–1; 2),
в котором лежат числа последовательности
(0 < an
< 2).
Существование предела полностью доказано.
Решая неравенство
x2
– x – 2 < 0, получим промежуток
(–1; 2),
в котором лежат числа последовательности
(0 < an
< 2).
Существование предела полностью доказано. |
|
|
|
Принцип сжатой последовательности. Если последовательности
(xn)
и
(zn)
сходятся к числу
а,
а последовательность
(yn)
такова, что при всех
n
выполняются неравенства
xn
≤ yn ≤
zn
то последовательность
(yn)
сходится к числу
а.
|
|
|
Нахождение
корней квадратного уравнения
Калькулятор выполнен в виде Java-скрипта.
Находится в коллекции свободного доступа и может быть включен в
HTML-страницу простым копированием.
This free script provided by JavaScript Kit
|
|
|
Задания. 1. Постройте
несколько членов рекуррентно заданной последовательности:
xn+1
= 1
+ 1/xn, x0
= 1.
2. Является ли последовательность монотонной?
3. Рассмотрите последовательности из чётных и нечётных членов
данной последовательности. Можно ли утверждать, что они монотонные?
Каков характер монотонности? 4*. Докажите
существования предела на основе принципа сжатой последовательности.
5. Найдите квадратное уравнение, один из корней которой
является пределом данной последовательности. |
3. Специальные приемы вычисления пределовМетод
разностей |
|
Пример. Найдем сумму
n
слагаемых:
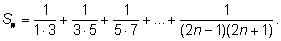
Представим первое слагаемое в виде
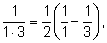 второе слагаемое
второе слагаемое
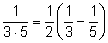 и т.д. Последнее слагаемое равно
и т.д. Последнее слагаемое равно
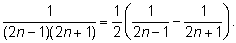 Теперь можно заметить, что
Теперь можно заметить, что
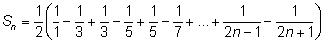 и все слагаемые, кроме первого и последнего
уничтожаются, следовательно,
и все слагаемые, кроме первого и последнего
уничтожаются, следовательно,
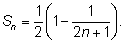
Второе слагаемое стремится к нулю, и
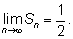
|
| |