| 1. Определение |
|
Геометрическую прогрессию называют бесконечно
убывающей, если ее знаменатель
q по модулю меньше единицы:
|q| < 1. |
|
Такое название возникло потому, что при
|q| < 1
общий член прогрессии
an =
a1qn – 1 становится
сколь угодно малым, «бесконечно убывает».
Найдем сумму бесконечно убывающей геометрической прогрессии с первым
членом
a1
и знаменателем
q (|q| <
1). Вычислим сумму
n
ее членов:
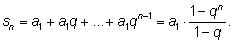 Разобьем
sn
на два слагаемых:
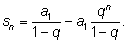
Первое слагаемое постоянно, а второе «бесконечно уменьшается» с
ростом
n.
При сложении «до бесконечности» мы отбрасываем эту добавку и
получаем формулу 
|
|
|
|
Упражнения.
1. Постройте бесконечно убывающую прогрессию
со знаменателем
0.9
(в качестве разделителя целой части от десятичной используйте
точку), используя явное задание последовательности (динамическая
модель слева). 2. Постройте
бесконечно убывающую прогрессию со знаменателем
0.9
(в качестве разделителя целой части от десятичной используйте
точку), используя рекуррентное задание последовательности
(динамическая модель справа). |
Проверяя эту формулу при
a1 =
1,
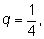получаем результат Архимеда: площадь параболического сегмента с
основанием
2
и высотой
1
равно
|
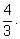
| 2. Обращение периодической десятичной
дроби в обыкновенную С помощью формулы суммы бесконечно
убывающей геометрической прогрессии легко обращать периодические
десятичные дроби в обыкновенные. |
Примеры
1. Обратить дробь
a =
1,444… = 1,(4)
в обыкновенную. Число
1,444…
– это запись суммы
1 + 0,4 + 0,04
+ 0,004 + … .
Сумму
0,4 +
0,04 + … можно рассмотреть как сумму
бесконечно убывающей геометрической прогрессии с первым членом
a1 =
0,4
и знаменателем
q = 0,1.
Выполняем подсчеты:
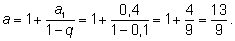
2.
а = 2,3(12) =
2,312121212… .
Запишем равенство:
a = 2,3 + 0,012
+ 0,00012 + … = 2,3 + 0,012 (1 + 0,01 + 0,012 + …).
В скобках стоит бесконечно убывающая геометрическая прогрессия со
знаменателем
q = 0,01.
Применяем формулу:
|
|
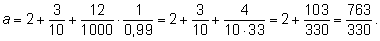
Теория пределов помогла обосновать многие рассуждения о суммировании
рядов, однако она не устранила всех противоречий, которые возникают,
если «легкомысленно» пользоваться этим понятием.
Рассмотрим, например, такой ряд:
1 – 1 + 1 – 1 +
…
Его частичные суммы попеременно равны то единице (при нечетных
n), то нулю (при четных
n):
1 = 1, 1
– 1 = 0, 1 – 1 + 1 = 1 и т. д.
Поэтому наш ряд не имеет суммы в смысле обычной теории пределов. |
| |