| 1. Схема вычисления производной |
|
Вычисление производной функции
у = f(x)
производится по следующей схеме:
1) Находим приращение функции на отрезке
 :
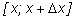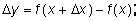
2) Делим приращение функции на приращение аргумента:
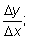
3) Находим предел
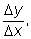устремляя
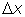к нулю. Переход к пределу мы будем записывать с
помощью знака
lim:
|
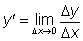
| 2. Примеры вычисления производных по
определению |
1. Производная линейной функции.
а)
у = С
— постоянная функция.
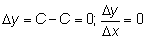
Так как отношение
постоянно и равно нулю, то производная
у тоже равна нулю:
у' = 0.
|
|
Итак, производная постоянной равна нулю:
С' = 0. |
б)
у = ах + b
— линейная функция.
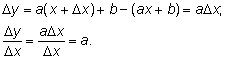
Как и в первом примере, отношение является постоянным. Поэтому в
качестве производной надо взять функцию, принимающую это постоянное
значение
а,
т. е.
у' = а.
|
|
Итак, производная линейной функции равна
коэффициенту при переменной:
(ах + b)' = а. |
|
2. Производная квадратичной функции
у = ах2.
|
|
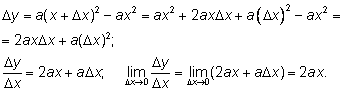
Упражнение. Закон движения имеет вид
s(t)
= at2/2 + v0 t + x0.
Используя динамическую модель движения, изучите особенности
графиков скорости
v(t)
(производной
s(t))
и ускорения
a(t)
(производной
v(t)).
Опишите их особенности и влияние на них
v0
и
x0 для следующих случаев.
1.
a>0
(меняя
v0
и
x0).
2.
a<0
(меняя
v0
и
x0).
3.
a=0
(меняя
v0
и
x0). |
|
|
| |
|
3. Производная функции
у = х3.
4. Производная функции
|
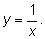
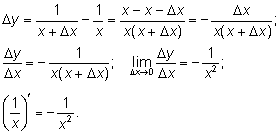
Во всех рассмотренных примерах находится производная рациональной
функции. При этом дробь
всегда можно сократить на
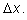Переход к пределу сводится к тому, что можно положить (после
сокращения)
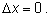
Рассмотрим более сложный пример.
5. Производная функции
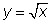
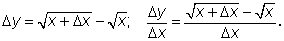
Для того чтобы сократить на
умножим числитель и знаменатель на сумму радикалов:
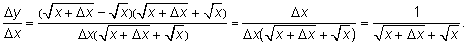
При маленьких
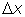значение корня
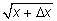близко к
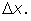Поэтому при переходе к пределу надо заменить в знаменателе
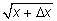на
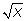
Получим:
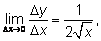т.е.
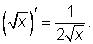
Производные, вычисленные в этих примерах, нужно запомнить: |
С' = 0;
(ах2)'
= 2ах;
|
| |
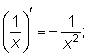
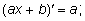
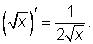