|
Большую часть своих усилий человек тратит на
поиск наилучшего, или, как часто говорят, оптимального, решения
поставленной задачи. Как, располагая определенными ресурсами,
добиться наиболее высокого жизненного уровня, наивысшей
производительности труда, наименьших потерь, максимальной прибыли,
минимальной затраты времени – так ставятся вопросы, над которыми
приходится думать каждому. Не все такие задачи поддаются точному
математическому описанию, не для всех из них найдены короткие пути
решения. Однако часть таких задач поддается исследованию с помощью
методов математического анализа – это задачи, которые можно свести к
нахождению наибольшего или наименьшего значения функции.
Наиболее важной для приложений ситуацией является
следующая: функция задана на отрезке
[а; b]
и имеет производную во всех точках этого отрезка. Тогда
для нахождения наибольшего и наименьшего значений этой функции надо
поступить так: найти критические точки (в данном случае корни
производной), вычислить значения функции во всех критических точках
и на концах отрезка, из найденных значений найти наибольшее и
наименьшее. |
|
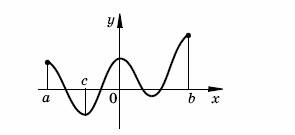 Функция,
график которой изображен на рисунке, задана на отрезке
[а; b]
и принимает наименьшее значение в точке
с
(одной из точек локального минимума), а наибольшее значение в точке
b
(крайней точке области определения). Функция,
график которой изображен на рисунке, задана на отрезке
[а; b]
и принимает наименьшее значение в точке
с
(одной из точек локального минимума), а наибольшее значение в точке
b
(крайней точке области определения).
|
| |
| Примеры 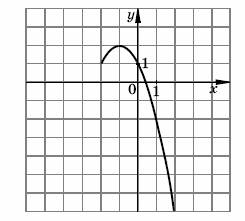 1.
Найти наибольшее и наименьшее значения функции 1.
Найти наибольшее и наименьшее значения функции
у = 1–2х - х2,
заданной на отрезке
[–2; 2].
Находим производную:
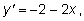 ее корни
(у' = 0
при
х = –1).
Вычисляем значения
у
в точках
2,–1,2:
ее корни
(у' = 0
при
х = –1).
Вычисляем значения
у
в точках
2,–1,2:
Получаем
yнаиб
= 2,
yнаим
= –7. При этом наибольшее значение
достигается в точке локального максимума, а наименьшее значение
функция принимает в точке на правом конце отрезка.
|
| |
|
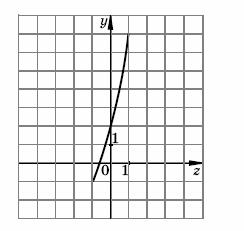 2.
Найти наибольшее и наименьшее значения функции 2.
Найти наибольшее и наименьшее значения функции
у = sin х +
4sin x + 2.
Для решения этой задачи не надо знать никаких свойств функции
у = sin х,
кроме того, что
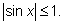 Сделаем замену
z = sin х
и рассмотрим функцию
у = z2
+ 4z + 2. Ее область определения –
отрезок
[–1; 1],
совпадающий с множеством значений функции
z = sin х.
Находим производную
у
как функции от
z
и корень этой производной:
у' = 2z + 4 = 0
Сделаем замену
z = sin х
и рассмотрим функцию
у = z2
+ 4z + 2. Ее область определения –
отрезок
[–1; 1],
совпадающий с множеством значений функции
z = sin х.
Находим производную
у
как функции от
z
и корень этой производной:
у' = 2z + 4 = 0
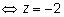
Заметим, что критическая точка не принадлежит отрезку
[—1; 1],
поэтому нам надо сравнить значения
у только на концах отрезка:
Итак,
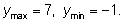
Многие прикладные задачи сводятся к нахождению наибольших и
наименьших значений функций, заданных на отрезке. Такие задачи часто
называют задачами на максимум – минимум.
|
| |
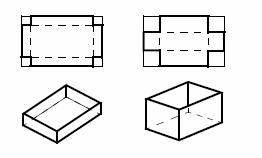 3.
Из прямоугольного листа жести размером
5 х 8
надо изготовить открытую коробку наибольшего объема, вырезая
квадратные уголки так, как показано на рисунке. 3.
Из прямоугольного листа жести размером
5 х 8
надо изготовить открытую коробку наибольшего объема, вырезая
квадратные уголки так, как показано на рисунке.
Обозначим через
х
длину стороны вырезаемого квадрата. Тогда длины сторон
прямоугольника уменьшатся на
2х
и объем коробки будет равен: 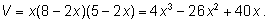
При этом
х
может меняться в следующих пределах:
0
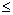 х х
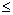 2,5.
Заметим сразу, что в крайних точках отрезка
[0; 2,5]
объем равен нулю. Находим критические точки: 2,5.
Заметим сразу, что в крайних точках отрезка
[0; 2,5]
объем равен нулю. Находим критические точки:
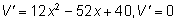 при
при
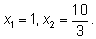
Отметим, что значение
х2
не принадлежит области определения.
При
х = 1
объем максимален:
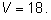
|
| |