| Таблицу первообразных получают с помощью таблицы
производных. Проверить таблицу можно, делая обратную операцию, т. е.
вычисляя производные. |
|
f(x)
|
 |
|
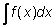1 |
x |
 |
|
 |
 |
  |
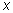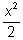
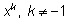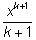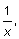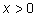In x |
|
sin x
|
– cos x
|
|
cos x
|
sin x
|
|
ex
|
ex
|
|
| Отметим полезные следствия, которые можно внести в
таблицу первообразных. |
|
|
|
Заметим, что операция дифференцирования известных
нам функций совершается формально – нужно запомнить несколько правил
и их будет достаточно для нахождения производных. Не так обстоит
дело с интегрированием, например, нет формулы для интегрирования
произведения и частного функций. Поэтому составлены обширные таблицы
интегралов (первообразных), и появляется новая задача – научиться
преобразовывать вычисляемые интегралы, сводя их к табличным. |
|
Пример.
Вычислить
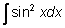
В таблице интегралов нет интеграла от
sin2
x.
Однако можно воспользоваться формулой
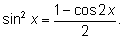Для
cos 2x
интеграл мы знаем, поэтому пишем так: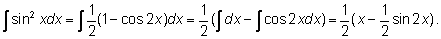 
|
| |
