|
Знаменитая теорема, одна из самых важных в
математическом анализе, названа именами его основоположников:
интеграл равен приращению первообразной.
Запишем формулировку более подробно. |
|
Теорема (Ньютона—Лейбница).
Пусть
f
— данная функция,
F—
ее произвольная первообразная. Тогда 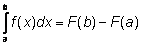
|
|
Доказательство. Сначала
проверим теорему, подставив в правую часть известную нам
первообразную для функции
f
– переменную площадь
S(x)
подграфика функции
f.
По определению интеграла
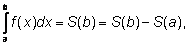 так как
S(a) = 0.
так как
S(a) = 0.
Пусть F — произвольная
первообразная для функции
f.
Тогда она отличается от
S
на константу, но приращение функций
F
и
S
будет одним и тем же: так как
S(x) =
F(x) + С,
то
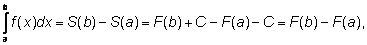
что и требовалось доказать. |
| Теорема Ньютона-Лейбница сводит вычисление интегралов к
вычислению первообразных. |
| Примеры.
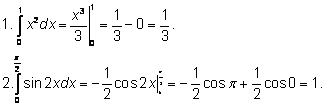
|
| |