| Формула Ньютона-Лейбница позволяет свести свойства
интеграла к свойствам первообразной, которые, в свою очередь, легко
получить, опираясь на свойства производной. |
|
Теорема (линейность интеграла).
|
|
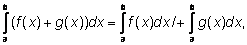
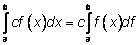
Доказательство. Пусть
F
и
G
– первообразные для функций
f
и
g
соответственно. Тогда функция
F
+ G является одной из первообразных
функции
f + g.
По теореме Ньютона-Лейбница
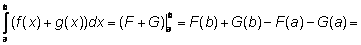
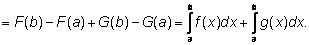
Вторая формула доказывается аналогично. |
Отметим полезные следствия выведенных свойств:
|
|
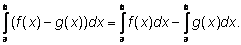
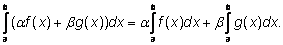
Ряд свойств интеграла является следствием свойств площади. |
|
Теорема (аддитивность интеграла).
|
|
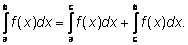
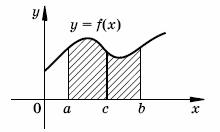 Это
свойство интеграла наглядно изображено на рисунке: площадь всей
криволинейной трапеции с основанием
[а; b]
есть сумма площадей трапеций с основаниями
[а; с]
и
[с; b].
Это же свойство можно получить и вычислением. Пусть
F
– первообразная для функции
f.
Тогда
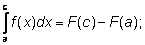
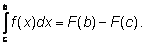
Складывая почленно левые и правые части равенств, получаем:
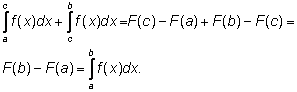
Доказанное свойство интеграла называют его аддитивностью (от
латинского слова addo – складываю).
Полезно отметить, что
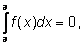так как
F(a) –
F(a) = 0.
|
|
Теорема (интегрирование неравенства).
Если
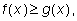то
|
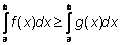
Действительно, функция
h(x) =
f(x) – g(x)
по условию неотрицательна. Следовательно, неотрицателен
и интеграл от нее, являющийся по определению площадью подграфика:
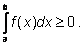
Раскрывая левую часть по свойствам
1
и
2,
получаем:
 
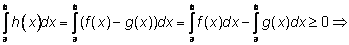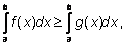что и требовалось доказать.
Примеры.
1.
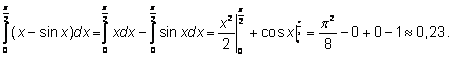
2.
|
| |
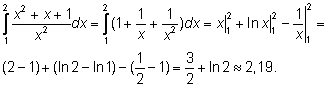