|
Рассмотрим испытание, имеющее конечное число
исходов, которые мы считаем одинаково возможными или,
как мы будем говорить дальше, равновероятными. Если
число равновероятных исходов равно
n,
то вероятность каждого из них мы принимаем за
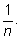 В примерах с подбрасыванием монеты, бросанием игральной
кости, вытаскиванием из колоды одной карты мы считаем исходы
равновероятными. Если в игральной кости сместить центр тяжести или
пометить рубашки некоторых карт, то исходы перестанут быть
равновероятными, чем часто пользуются с целью обмана.
В примерах с подбрасыванием монеты, бросанием игральной
кости, вытаскиванием из колоды одной карты мы считаем исходы
равновероятными. Если в игральной кости сместить центр тяжести или
пометить рубашки некоторых карт, то исходы перестанут быть
равновероятными, чем часто пользуются с целью обмана.
Выберем из
n
равновероятных исходов случайного испытания какие-то
m
исходов, в которых мы заинтересованы, или, как мы будем говорить
дальше, которые мы считаем благоприятными.
Вероятностью наступления благоприятного исхода считают дробь
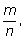 где
n
– общее число равновероятных исходов, а
m
– число благоприятных.
где
n
– общее число равновероятных исходов, а
m
– число благоприятных. |
|
Пример. Выберем случайным
образом одну букву из слова абракадабра. В этом слове
11
букв и выбор каждой из них равновероятен. Так как буква
а
встречается
5
раз, то вероятность
ра
того, что выбранной буквой окажется именно
а,
равна
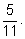 Выпишем вероятности для других букв:
рб
=
Выпишем вероятности для других букв:
рб
=
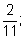 рр =
рр =
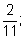 рк =
рк =
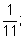 рд
=
рд
=
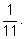 Заметим, что сумма всех дробей
ра + рб
+ рр + рк + рд
равна единице. Если мы возьмем букву, не встречающуюся
в нашем слове, например,
в,
то для нее вероятность будет равна нулю:
рв =
0, так как число благоприятных исходов
равно нулю. Можно предусмотреть такой благоприятный исход –
выбранная буква является согласной. Вероятность
р
такого исхода равна
Заметим, что сумма всех дробей
ра + рб
+ рр + рк + рд
равна единице. Если мы возьмем букву, не встречающуюся
в нашем слове, например,
в,
то для нее вероятность будет равна нулю:
рв =
0, так как число благоприятных исходов
равно нулю. Можно предусмотреть такой благоприятный исход –
выбранная буква является согласной. Вероятность
р
такого исхода равна
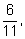 так как среди
11
букв
6
являются согласными. Более сложное событие – выбор согласной буквы –
распадается на независимые друг от друга элементарные события
– выбор буквы
б,
буквы
р,
буквы
к
или буквы
д.
Заметим, что сумма вероятностей
рб +
рр + рк + рд =
так как среди
11
букв
6
являются согласными. Более сложное событие – выбор согласной буквы –
распадается на независимые друг от друга элементарные события
– выбор буквы
б,
буквы
р,
буквы
к
или буквы
д.
Заметим, что сумма вероятностей
рб +
рр + рк + рд =
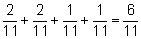 как раз и равна
р.
как раз и равна
р.
Два события – выбор согласной буквы
или выбор гласной буквы – являются противоположными друг другу (мы
считаем, что каждая рассматриваемая буква является гласной или
согласной). Ясно, что сумма их вероятностей должна получиться равной
единице, что легко проверяется: гласная буква лишь одна и
вероятность ее выбора равна
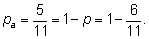
|
|
Следующие пять примеров существенно сложнее.
Приписывание определенных вероятностей результату стрельбы или
характеру завтрашней погоды – вещь достаточно произвольная, хотя и
должна выполняться с соблюдением определенных правил (свойств
вероятности), которые мы опишем чуть позже. Естественно считать, что
это приписывание должно основываться на предыдущем опыте, т. е. на
анализе уже известных статистических данных. |
|
Событие, вероятность которого равна нулю (например,
выбор цифры
1
из записи числа
232),
называют невозможным событием. Событие, вероятность
которого равна единице (например, выбор цифры
1
из записи числа
111),
называют достоверным.
Событие, которому соответствует один благоприятный исход, можно
назвать элементарным, или простым событием. |
| Например, если
А1
и
А2
– элементарные события, то событие
А3:
«происходит
А1
или
А2»
или
А4:
«происходят одновременно
А1
и
А2»
являются сложными, составленными из простых событий
А1
и
А2
по определенным правилам. |
| |