| 1. Свойства вероятностей.
Рассмотрим испытание, имеющее
n равновероятных исходов. Выберем
m из
них, которые будем считать благоприятными, и рассмотрим событие
А, состоящее в наступлении благоприятного исхода. |
|
Вероятность
рА события А равна по определению дроби
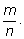
|
|
Перечислим первые простейшие свойства вероятности.
1)
0
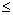 рА
рА
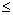 1.
1.
2) Если событие А невозможно (т. е. если
m = 0), то рА = 0; если событие
А достоверно (т. е.
если
m = n), то рА = 1.
3) Если событие
В состоит в том, что не наступает
событие А, т. е. если оно является противоположным
событию
А,
то
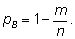
Действительно, если
m исходов благоприятны для события
А, то остальные
n – m – неблагоприятны. Событие
В как раз и состоит в наступлении одного из этих
n – m исходов, т. е.
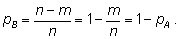
|
|
2. Вычисление вероятностей в
случае равновероятных исходов.
Для вычисления вероятности по приведенному определению приходится
решать комбинаторные задачи – находить общее число равновероятных
исходов и число благоприятных исходов.
|
|
Пример 1
Одновременно бросают две игральные кости. Какова вероятность, что на
них в сумме выпадет 6 очков?
Возможные исходы испытания таковы: может выпасть в сумме
2,
3, …, 12 очков, т. е. общее количество исходов равно
11. Однако если в первом примере все перечисленные исходы были
равновероятны (это подчеркивалось тем, что каждая буква слова
пишется независимо от предыдущих), то сейчас, конечно, нет.
Совершенно ясно, что сумму
2 или
12 получить
труднее, чем сумму
6. Разобьем событие (сумма очков на
двух костях) иначе, т. е. выделим иные элементарные события, которые
будут равновероятными. Представим себе, что мы различаем между собой
кости (скажем, покрасим их в разные цвета) и запишем исход испытания
в виде упорядоченной пары чисел от 1 до 6, показывающей, сколько очков выпало на каждой кости. Ясно теперь, что
эти исходы равноправны, равновероятны, и их количество равно
62 = 36. Для нахождения числа благоприятных исходов (таких пар
(a; b), что
a + b = 6) придется перебрать все
36 комбинаций, что сделано в следующей таблице.
|
b
a |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Из таблицы видно, что сумма 6 встречается
5 раз. Искомая вероятность равна
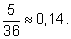
Для интереса выпишем вероятности px для всех сумм
x от
2 до
12:
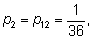
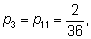
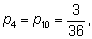
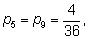
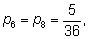
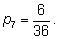
|
|
|
|
|
|
Модель кости выполнена в виде Java-скрипта.
Находится в коллекции свободного доступа и может
быть включен в HTML-страницы
простым копированием.
This free script provided by
JavaScript Kit (в скрипте обнаружены и исправлены математические ошибки)
|
|
3. Вероятность суммы несовместных событий.
С помощью примера
1 можно проиллюстрировать еще одно
простое, но важное свойство вероятности, которое мы обсудим в
следующем примере. |
|
Пример 2
Бросают две игральные кости. Какова вероятность, что в сумме на них
выпадет не больше четырех очков?
Сложное событие (выпадает не больше четырех очков) можно разбить на
более простые: выпадет
2, 3 или 4 очка.
При этом важно следующее: если произошло сложное событие (выпало не
более четырех очков), то произошло хотя бы одно из более простых
событий (выпало 2, или выпало
3, или выпало
4 очка); никакие два из них не могут произойти одновременно (эти
события несовместны). В таком случае говорят, что
событие А (выпало не более четырех очков) представлено в
виде суммы несовместных событий
А2 (выпало
2 очка), А3 (выпало 3 очка) и
А4
(выпало 4 очка). Ясно, что
рА = р2 + р3 + р4 =
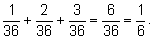
|
|
Итак, можно сформулировать следующее свойство вероятностей: |
|
Если событие
А можно
представить в виде суммы нескольких попарно несовместных событий, то
его вероятность равна сумме вероятностей этих событий (теорема о
сумме вероятностей). |
|
Применение этого правила требует отчетливого
осознания того, что означает сумма событий и что означает их
несовместность.
Заметим, в частности, что если достоверное событие (например, мы
бросили пару игральных костей и выпадет какое-нибудь число) разбить
в сумму попарно несовместных событий (получим одну из сумм от
2 до
12), то сумма вероятностей этих событий равна
единице:
р2 + р3 + … + р11 + р12 = 1.
Этим правилом часто пользуются при проверке того, все ли случаи
учтены при переборе исходов. Например, если, вычисляя вероятности
различных (несовместных между собой) исходов, мы видим что их сумма
меньше единицы, это означает, что какой-то возможный исход оказался
неучтенным. |
|
|
|
Модель кости выполнена в виде Java-скрипта.
Находится в коллекции свободного доступа и может
быть включен в HTML-страницы
простым копированием.
This free script provided by
JavaScript Kit (в скрипте обнаружены и исправлены математические ошибки)
|
| |