| 1. Схема Бернулли.
Ситуация, в которой подряд независимо друг от друга производятся
одинаковые испытания, встречается очень часто, например, бросание
монеты или игральной кости, стрельба из одного орудия без учета
результата произведенных выстрелов, параллельное включение в сеть
одинаковых предохранителей и т. п. Разберем более подробно пример с
бросанием монеты. При каждом испытании есть два равновероятных
исхода:
О
(выпал орел) и
Р
(выпала решка). Допустим, что монету бросили подряд
n
раз. Сколько последовательностей исходов при этом можно получить?
Эта комбинаторная задача фактически уже была решена раньше.
Последовательность результатов испытаний можно записать как слово в
двухбуквенном алфавите, например
ОРРОР.
Число
n
-буквенных слов в таком алфавите равно
2n.
Таким образом, общее число возможных вариантов при повторном
бросании монеты будет равно
2n.
Какова вероятность того, что при
n-кратном
бросании монеты все время будет выпадать орел? Ясно, что из всех
возможных
2n
вариантов благоприятным является один:
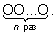 Искомая вероятность равна
Искомая вероятность равна
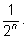
|
Например, при
n = 10
эта вероятность равна
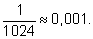
|
|
Возьмем
n = 3.
Если нас интересует только то, сколько раз выпадет орел (или решка),
то возможные варианты будут такими:
1)
три раза;
2)
два раза;
3)
один раз;
4)
ни одного раза. Вероятности этих событий равны соответственно
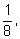
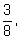
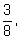
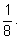 Проводя перебор вариантов для
n = 4,
мы получаем такой набор вероятностей:
Проводя перебор вариантов для
n = 4,
мы получаем такой набор вероятностей:
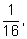
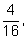
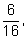
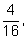
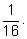 Нетрудно заметить, что в числителях стоят элементы
треугольника Паскаля.
Нетрудно заметить, что в числителях стоят элементы
треугольника Паскаля.
Составим таблицу. Она получается из треугольника
Паскаля делением каждой строки на соответствующую степень двойки, то
есть сумму чисел в этой строке, и представляет таблицу вероятностей
различных исходов при повторном бросании монеты.
|
Пусть событие
A
происходит с вероятностью
p.
Запишем разложение бинома:
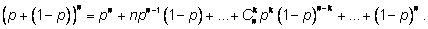
Слагаемое
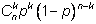 дает вероятность того, что при повторном
n
-кратном испытании событие
A
наступит ровно
k
раз.
дает вероятность того, что при повторном
n
-кратном испытании событие
A
наступит ровно
k
раз.
В частности, при
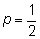 наступление и ненаступление события
A
при каждом испытании равновероятны.
наступление и ненаступление события
A
при каждом испытании равновероятны.
|
Примеры
Пусть монета брошена
6
раз.
1. Вероятность того, что хоть раз выпал орел:
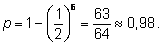
2. Вероятность того, что орел выпадет столько же раз, сколько и
решка:
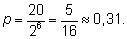
3. Вероятность того, что орел выпадет не менее трех раз:
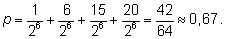
Рассмотренная схема повторных испытаний основана на некоторых новых
для нас свойствах вероятности. |
|
2. Вероятность произведения независимых событий.
Рассмотрим два независимых друг от друга события
А
и
В.
Пусть событие
С
состоит в том, что происходят события
А
и
В
(такое событие
С
называют произведением событий
А
и
В).
Если вероятность события
А
наступает в
m1
случаях из
n1
возможных (то есть вероятность
p1
= m1 / n1),
а событие
В
в
m2
случаях из
n2
(p2
= m2 / n2)
и если эти события происходят независимо друг от друга, то
вероятность
p
наступления двух событий
А
и
В
равна m1m2
/ n1n2
(теорема о произведении вероятностей, основанная на
комбинаторном правиле произведения).
Можно записать эту теорему формулой
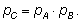
Применяя эту формулу, можно вычислить вероятность сложного события.
Пусть в последовательности из
n
испытаний событие
A
наступает с вероятностью
p.
Тогда вероятность, что событие
А
наступит в каждом из
k
испытаний и не наступит (то есть произойдет событие
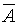 с вероятностью
1 – p) в каждом из остальных испытаний, равна
с вероятностью
1 – p) в каждом из остальных испытаний, равна
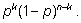 |
| 3. Обоснование формулы вычисления
вероятностей в схеме Бернулли. Теперь
можно более точно обосновать формулу для вероятности
pk
того, что при повторном
n
-кратном испытании событие
А,
наступающее с вероятностью
р,
появилось ровно
k
раз:
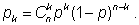
Действительно, если мы зафиксируем номера испытаний, когда
произойдет и когда не произойдет событие
А,
то получим вероятность, равную
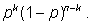 Так как фиксировать набор из
k
номеров можно
Так как фиксировать набор из
k
номеров можно
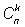 способами, то, применяя теорему о сумме вероятностей, получим
требуемую формулу.
способами, то, применяя теорему о сумме вероятностей, получим
требуемую формулу. |
|
Случайное бросание монеты
|
| |