| 1. Понятие геометрической вероятности
Приписывание событию некоторого числа (его вероятности) является
аналогом измерения. В тех случаях, когда поле исходов события
бесконечно, естественно связать определение вероятности с геометрией.
Например, при случайном выборе точки в круге, разделенном на
несколько колец, вероятностью попадания в заданное кольцо
естественно считать долю, которую занимает площадь
выбранного кольца по отношению к площади всего круга. В примере о
том, дождется ли пассажир автобуса, если у него ограничено время
ожидания, на первый взгляд, неясно, как определить вероятность этого
события. Один из возможных путей состоит в том, чтобы построить
некоторую геометрическую модель и связать вероятность с
геометрическими измерениями. |
|
 Например,
если по оси
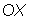отложить интервал времени
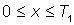между двумя приходами автобуса на остановку, а по оси
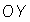интервал времени, в течение которого может появиться на остановке
пассажир, например,
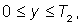то точки с координатами
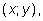где
x
– момент появления автобуса на остановке,
y
– момент появления пассажира, заполнят прямоугольник со сторонам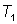и
и
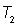и площадью
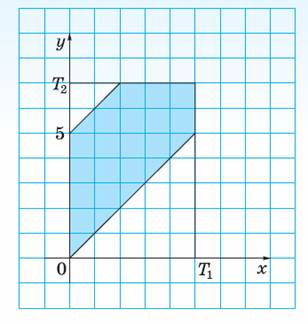
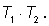Очевидно, что пассажир дождется автобуса, если автобус появится на
остановке после появления там пассажира и не более чем через
5
минут после его прихода (время ожидания пассажиром автобуса),
следовательно, должно выполняться неравенство:
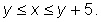Теперь осталось выяснить, какую часть прямоугольника заполнят точки,
координаты которых удовлетворяют этому неравенству.
|
|
Пусть некоторая плоская фигура разбита на
несколько непересекающихся частей. Рассмотрим испытание – выбор
точки в этой фигуре. Возможными исходами будем считать попадание
точки в одну из этих частей. Каждому такому исходу можно приписать
вероятность, равную отношению площади части, в которой находится
точка, к площади всей фигуры.
Аналогичные определения можно дать для вероятностей попадания точки
в заданную часть данного отрезка прямой (или кривой линии),
определенную с помощью измерения длины или – для случая
пространственной фигуры – с помощью измерения объема.
|
|
2. Примеры вычисления геометрической вероятности
1. В квадратном трехчлене
x2 +
6x + a коэффициент
а
по модулю не больше
10.
Он выбирается наудачу. Какова вероятность того, что трехчлен будет
иметь вещественные корни?
Дискриминант
d
этого трехчлена равен
32 –
a = 9 – a.
Условие вещественности корней:
d
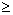0
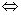a
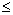9. На отрезке
[–10;
10], длина которого равна
2 0,
«благоприятные» значения а занимают отрезок
[–10; 9],
длина которого
19.
Интересующему нас событию следует приписать вероятность
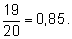
2.
В круге произвольно выбирается точка. Какова вероятность того, что
ее расстояние до центра круга больше половины?
Построим две концентрические окружности радиуса R и
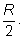Площадь маленького круга равна
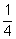площади большого, а площадь кольца между ними – 
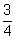площади большого. Вероятность попадания точки в кольцо
следует принять равной
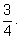
Заметим, что мы игнорируем границы наших областей.
Если вероятность мы измеряем площадью, то вероятность попадания
точки на границу области равна нулю, так как площадь границы должна
быть нулевой. |
| 3. Построение вероятностной модели.
Часто в приложениях для определения вероятности события приходится
строить геометрическую модель и изображать событие точками
геометрической фигуры. |
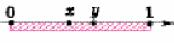 Палку
ломают случайным образом в двух точках. Какова вероятность того, что
из трех получившихся кусков можно составить треугольник?
Построение модели. Пусть длина палки равна
1.
Можно сказать, что на единичном отрезке выбирают две точки
x
и
y.
Случайное событие выбора пары точек можно изобразить точкой в
единичном квадрате на плоскости
xOy.
Условие того, что из получившихся отрезков можно сложить треугольник,
можно записать в виде серии неравенств (будем сразу считать, что
x
и
y
обозначены так, что
x < y).
Эти условия таковы:
1)
x + y – x
> 1 – y
2)
x + 1 – y > y –
x
3)
y – x + 1 – y >
x
Построим область в единичном квадрате, для точек которой выполняются
все написанные условия. Мы получим треугольник, площадь которого,
как нетрудно проверить, равна
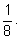Искомая вероятность равна отношению
|
| |
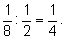