|
1. Понятие математического
ожидания
Представим себе, что в беспроигрышной лотерее разыгрывается шесть
призов стоимостью
а1,
а2, …, а6
рублей. Выпадение любого из шести номеров разыгрываемых призов
равновероятно. На какой выигрыш в среднем может рассчитывать человек,
многократно участвующий в лотерее и каждый раз обладающий одним
билетом? Ясно, что ожидаемым выигрышем надо считать среднее
арифметическое стоимостей призов, то есть число
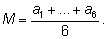 |
|
Это число и называют математическим ожиданием
выигрыша. |
|
Рассмотрим более сложную ситуацию, когда
возможные исходы испытания не являются равновероятными. Пусть,
например, при розыгрыше трех призов стоимостью
а1,
а2 и
а3
вероятности выигрыша их равны соответственно
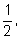
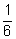 и
и
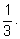 (То, что
(То, что
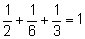 говорит о том, что должна наступить ровно одна из
предполагаемых возможностей). Тогда для определения математического
ожидания выигрыша надо числа
а1,
а2 и
а3
взять с весами, равными вероятностям выигрыша соответствующего приза,
то есть взять число
говорит о том, что должна наступить ровно одна из
предполагаемых возможностей). Тогда для определения математического
ожидания выигрыша надо числа
а1,
а2 и
а3
взять с весами, равными вероятностям выигрыша соответствующего приза,
то есть взять число
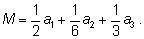 |
|
Рассмотрим задачу де Мере о справедливом разделе
банка. Пусть в игре, состоящей из последовательной серии партий, в
каждой из которых выигрывает один из игроков, участвовало три игрока.
Выигрывает банк тот, кто первым оказывается победителем в четырех
партиях. Игра была прервана после шести партий, в одной из которых
выиграл первый игрок, в двух – второй и в трех – третий. Как им
справедливо разделить банк? Это и есть задача определения
математического ожидания выигрыша для каждого игрока. Ситуация здесь
простая – если мы найдем вероятности первым выиграть четыре партии (после
уже состоявшихся шести партий) для каждого из игроков, то весь банк
и надо разделить пропорционально этим вероятностям.
Итак, первому игроку осталось выиграть три партии, второму две и
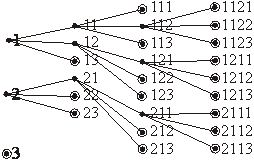
третьему одну. Попробуем решить задачу просто перечислением
вариантов. Будем выписывать в виде «дерева» все равновероятные
возможности. Цифра означает номер игрока, выигравшего в очередной
партии. |
№ партии
1
2
3
4
 |
|
Кружками обозначены ситуации, когда кто-либо (он
указан последним) выиграл четыре партии. Вероятности ситуаций в
первой колонке равны
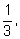 во
второй – во
второй –
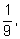 в
третьей – в
третьей –
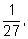 в
четвертой – в
четвертой –
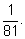
Вероятность выигрыша каждого из участников складывается из
вероятностей всех ситуаций, где он завершает игру.
1:
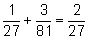 (он
завершает игру в одном случае после трех партий и в трех случаях
после четырех) (он
завершает игру в одном случае после трех партий и в трех случаях
после четырех)
2:
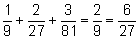
3:
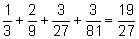
В итоге банк надо разделить в пропорции
2 : 6 : 19.
Математические ожидания выигрышей каждым игроком равны
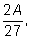
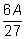 и
и
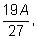 где
А
– величина банка.
где
А
– величина банка.
Пусть случайное событие
А
состоит в появлении одного из числовых значений
А1,
А2, …, с вероятностями
p1,
p2, …,
(
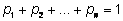 ).
Математическим ожиданием события
А
называют число ).
Математическим ожиданием события
А
называют число
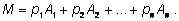
В случае, когда исходы равновероятны, т. е. когда все
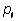 равны
равны
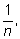 математическое ожидание
М
равно среднему арифметическому
математическое ожидание
М
равно среднему арифметическому
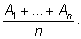
Пусть в игре возможны два исхода – выигрыш и
проигрыш. Пусть
p
– вероятность выигрыша, причем величина выигрыша равна
а.
Тогда вероятность проигрыша равна
1 – p,
его величину будем считать равной
(–b).
Число
M = ap– b(1 –
p)
называется математическим ожиданием результата игры.
Если
М > 0,
то игрок будет в выигрыше, если
M < 0
– то в проигрыше. Например, если вероятность выигрыша равна
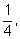 но в случае выигрыша он получает в пять раз больше, чем теряет в
случае проигрыша, то математическое ожидание вычисляется так:
но в случае выигрыша он получает в пять раз больше, чем теряет в
случае проигрыша, то математическое ожидание вычисляется так:
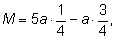 где
а
– величина ставки. Так как
где
а
– величина ставки. Так как
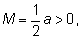 то математическое ожидание положительно и игроку стоит
рисковать.
то математическое ожидание положительно и игроку стоит
рисковать. |
| |