|
1. Умножение комплексных чисел в
тригонометрической форме
Тригонометрическая форма комплексного числа позволяет дать
геометрическую интерпретацию умножения комплексных чисел. Запишем
два комплексных числа в тригонометрической форме и перемножим их:
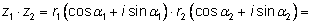
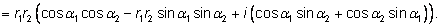
Мы узнаем в скобках формулы для косинуса и синуса
суммы углов
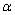 1
и 1
и
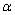 2: 2:
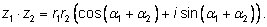
Получилось комплексное число в тригонометрической форме. Итак, при
умножении комплексных чисел их модули перемножаются, а аргументы
складываются.
Если числа
z1
и
z2
изображены на комплексной плоскости, то
их произведение можно изобразить так: надо построить окружность (с
центром в начале координат) радиуса
r1r2,
затем взять подвижный луч и повернуть его на
угол
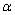 1
+ 1
+
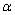 2.
Точка пересечения этого луча с построенной окружностью и будет
изображением произведения
z1z2. 2.
Точка пересечения этого луча с построенной окружностью и будет
изображением произведения
z1z2.
Формула умножения комплексных чисел в тригонометрической форме
применима к произведению любого числа комплексных чисел – правило
остается тем же: модули перемножаются, а аргументы складываются. |
|
2. Деление комплексных чисел в
тригонометрической форме.
Заметим, что можно использовать тригонометрическую форму
комплексного числа не только для умножения, но и для деления
комплексных чисел. Если
z = r (cos
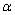 + i sin
+ i sin
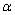 ),
то z–1 = r–1 (cos (– ),
то z–1 = r–1 (cos (–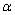 )
+
i sin (– )
+
i sin (–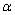 )).
Действительно, перемножим числа
r (cos )).
Действительно, перемножим числа
r (cos
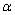 + i sin
+ i sin
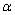 )
и )
и
r–1
(cos (–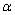 )
+ i sin (– )
+ i sin (–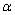 )),
получим: )),
получим:
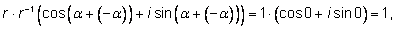 т. е. указанное нами число есть
т. е. указанное нами число есть
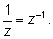
Деление
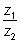 – это умножение
z1
на
z2–1.
Получим
– это умножение
z1
на
z2–1.
Получим
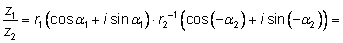
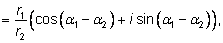 т. е. при делении комплексных чисел их модули делятся
друг на друга, а аргументы вычитаются.
т. е. при делении комплексных чисел их модули делятся
друг на друга, а аргументы вычитаются.
|
| |