|
Уравнение – это два выражения с
неизвестными, соединенные знаком равенства.
Неизвестное – это буква для обозначения какой-либо
неизвестной величины.
Составление уравнения. В ходе анализа задачи составляются
выражения с неизвестными, которые можно приравнять друг другу,
исходя из заданных условий. |
|
Составление уравнения, описывающего,
моделирующего поставленную задачу, обычно начинается с выбора и
обозначения неизвестных. При этом стремятся сократить число
неизвестных, найти для них удобные и понятные обозначения. |
|
Область допустимых значений (ОДЗ) – это
множество значений, которые могут принимать неизвестные, входящие в
уравнение. ОДЗ уравнения определяется, с одной стороны, множеством
рассматриваемых значений неизвестных, а с другой стороны, – тем,
чтобы были осмыслены все операции, с помощью которых составлено
уравнение. |
|
Так, например, уравнение для числа
п сторон
многоугольника, имеющего данное число
а
диагоналей, запишется в виде
|
|
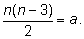
По смыслу задачи неизвестное может принимать в
качестве значений натуральные числа, большие или равные трем. В то
же время сами операции, входящие в уравнение, не накладывают
дополнительных условий на
ОДЗ уравнения. |
|
Взяв, например, значение
а = 8, мы
получим квадратное уравнение
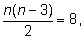которое имеет корни, но они не входят в
ОДЗ, так как
являются иррациональными числами. В то же время в
ОДЗ
уравнения
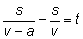для нахождения неизвестной скорости
v при
заданных величинах
s, t и
а (помимо
требований к скорости
v, вытекающих
из смысла задачи) надо включить условия
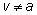и
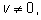так как при этих значениях
v сама
запись уравнения теряет смысл. |
|
Процесс составления уравнения часто называют
моделированием, построением математической модели поставленной
задачи, при этом приходится делать определенные допущения (предположения).
Так, при составлении математической модели движения подбрасываемого
мячика мы обычно пренебрегаем его размерами (считаем его точкой), не
учитываем сопротивление воздуха или изменение силы тяжести с высотой
и т. п. Полученное уравнение является возможной математической
моделью движения мячика, описывающей его движение с некоторой
точностью. |
|
Решение уравнения – это набор значений
неизвестных (из
ОДЗ), при
подстановке которых уравнение превращается в верное числовое
равенство.
Корень уравнения – это другое название для решения уравнения,
употребляемое для уравнений с одним неизвестным. |
|
Задача решения уравнения сводится к описанию
множества его решений. Это описание допустимо в различных формах.
Можно использовать теоретико-множественные обозначения. Тогда запись
ответа в виде множества
X
решений уравнения может выглядеть, например, так:
X = {2};
X = {2; 5; 10};
X = [0; 1];
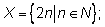
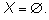
Общепринятая запись множества с помощью перечисления его элементов в
фигурных скобках часто оказывается громоздкой, и можно использовать
любую другую форму записи, лишь бы она была точной и понятной. |
|
Решить уравнение – значит, найти, описать
все решения уравнения. |
| При этом может оказаться, что уравнение решений не
имеет, множество его решений пусто. |
|
Исследование уравнения. В исследование
уравнения могут включаться различные вопросы о поведении его решений.
Система уравнений – это набор нескольких уравнений.
Решить систему уравнений – найти решения, которые
удовлетворяют каждому из уравнений. |
Обозначение системы:
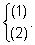Естественно, что уравнений, входящих в систему, может быть больше
двух.
|
|
Совокупность уравнений – это также набор
нескольких уравнений, но при этом требуется найти решения, которые
удовлетворяют хотя бы одному из уравнений. Обозначение:
|
| |
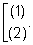