|
Равносильность уравнений. Два уравнения
(1) и
(2)
называются равносильными, если мно¬жества их решений совпадают, т.
е. если каждое решение уравнения
(1)
является решением уравнения
(2), и
обратно – всякое решение уравнения
(2)
является решением уравнения
(1). |
Знак равносильности:
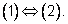 |
|
Уравнение
(1) называется
следствием уравнения
(2), если
всякое решение уравнения
(2) является
решением уравнения
(1). |
Знак следствия:
(2)
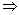 (1) (1)
|
|
Два уравнения равносильны тогда и только тогда,
когда каждое из них является следствием другого. |
|
Действия, сохраняющие равносильность. Если
к двум частям уравнения прибавить одно и то же число или их умножить
на одно и то же число, отличное от нуля, то получится уравнение,
равносильное исходному. |
Получение следствий. Следующие преобразования приводят к
следствию данного уравнения:
– умножение обеих частей уравнения на одно и то же выражение, не
уменьшающее ОДЗ уравнения;
– возведение обеих частей уравнения в квадрат (или в одну и ту же
степень).Нарушение равносильности.
Следующие преобразования могут нарушить равносильность уравнений (изменить
множество его корней):
– преобразования, изменяющие ОДЗ уравнения (взаимное уничтожение
членов, сокращение дробей, прибавление к обеим частям уравнения
одного и того же выражения, возведение в квадрат или другую четную
степень и т. п);
– преобразования, которые могут вызвать появление посторонних корней
(умножение обеих частей уравнения на одно и то же выражение – за
счет корней этого выражения, возведение в квадрат или другую четную
степень – за счет «потери знака», так как неверное равенство
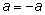 может перейти в верное
может перейти в верное 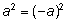 и т. п.);
и т. п.);
– преобразования, которые могут вызвать потерю корней (сокращение
обеих частей уравнения на общий множитель – за счет корней этого
множителя; извлечение квадратного кор¬ня из двух частей уравнения
без учета знака – за счет того, что из равенства
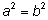 может следовать как
может следовать как
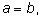 так и
так и
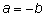 и т. п.).
и т. п.). |
Логическая связь между уравнениями может быть записана
с помощью отношений между множествами их решений. Пусть множества
решений уравнений
(1) и
(2) обозначены
соответственно
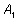 и
А2.
и
А2.
|
Логическая связь |
Термин |
Множество
решений |
|
(1)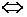 (2) (2) |
Равносильность |
А1
=А2
|
|
(2)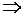 (1) (1) |
Следствие
|
 |
|
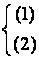 |
Система
|
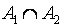 |
|
|
 |
Совокупность
|
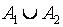 |
|
|
Связь между понятиями равносильности и следствия
также может быть выражена на языке теории множеств:
(1)
 (2)
означает, что
(2) (2)
означает, что
(2)
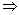 (1)
и
(1) (1)
и
(1)
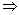 (2);
А1 =А2
означает, что (2);
А1 =А2
означает, что
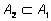 и
и
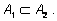 |
Примеры нарушения равносильности.
|
|
В первом примере взаимное уничтожение членов
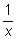 и
и
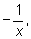 стоящих в одной части уравнения не входит в ОДЗ исходного. То же
самое мы видим во втором, третьем и четвертом примерах. В пятом
примере корень
стоящих в одной части уравнения не входит в ОДЗ исходного. То же
самое мы видим во втором, третьем и четвертом примерах. В пятом
примере корень
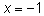 второго уравнения не входит в ОДЗ первого уравнения. В шестом
примере умножение на
второго уравнения не входит в ОДЗ первого уравнения. В шестом
примере умножение на
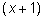 привело к лишнему корню
привело к лишнему корню
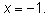 В седьмом примере появился посторонний корень
В седьмом примере появился посторонний корень
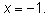 В восьмом примере при делении на
В восьмом примере при делении на 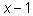 потерялся корень
потерялся корень
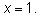 В девятом примере при извлечении квадратного корня
потерялся корень
В девятом примере при извлечении квадратного корня
потерялся корень
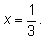 |
| |