| 1. Понятие алгебраического уравнения |
|
Алгебраическими уравнениями называют уравнения,
которые равносильными преобразованиями могут быть приведены к
уравнению вида
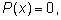 где
где 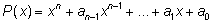 – многочлен. Его степень называют степенью уравнения. Корни
многочлена
Р – это и есть
корни исходного уравнения.
– многочлен. Его степень называют степенью уравнения. Корни
многочлена
Р – это и есть
корни исходного уравнения. |
|
Формулы для корней уравнений второй степени (квадратных
уравнений) требуют извлечения квадратного корня из некоторого
выражения, составленного из коэффициентов многочлена – его
дискриминанта
D. Если мы
интересуемся действительными корнями, то они существуют лишь при
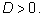 При
При
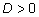 формулы дают два разных корня, при
формулы дают два разных корня, при
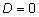 корень единственный. При
корень единственный. При
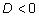 квадратное уравнение действительных корней не имеет.
квадратное уравнение действительных корней не имеет.
Основной способ решения алгебраических уравнений состоит в том,
чтобы с помощью замен неизвестного и разложения на множители свести
его к решению цепочки линейных и квадратных уравнений. Можно сказать,
что уравнение вида
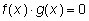 равносильно совокупности уравнений
равносильно совокупности уравнений
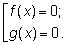
При этом надо следить за тем, чтобы при «расщеплении» одного
уравнения на два сохранялась
ОДЗ
исходного уравнения. |
2. Примеры
1. Линейное уравнение
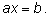 Решение
Решение
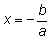 при
при
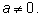
2. Уравнение с модулем
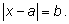 Решение
Решение
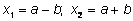 при при
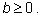
3. Степенное уравнение
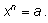 Решение
Решение
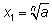 при
при
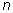 нечетном;
нечетном;
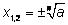 при
при
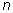 четном и
четном и
4. Квадратное уравнение
1)
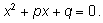 Решение
Решение
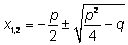 при
при
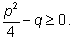
2)
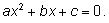 Решение
Решение
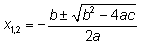 при
при
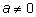 и
и
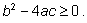
|
|
Упражнение. Используя
калькулятор для нахождения корней кубического
уравнения с ненулевым свободным членом, выполните следующие задания.
1. Составьте уравнение, имеющие корень
x
= 1.
Проверьте ответ.
2. Составьте уравнение, имеющие корни
x =
1 + i
и
x = 1 - i.
Проверьте ответ. |
|
Автор скрипта Stephen R. Schmitt.
Скрипт разрешён к
модификации и свободному распрстранению.
|
|
3. Наиболее типичные приемы решения уравнений.
1. Разложение на множители. Если уравнение можно
привести к виду
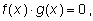 то его решения являются объединением решений двух уравнений
то его решения являются объединением решений двух уравнений
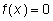 и
и
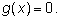
2. Замена неизвестного. Если уравнение можно привести
к виду
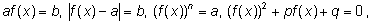 то можно сделать замену неизвестного
то можно сделать замену неизвестного
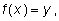 получить и решить стандартное уравнение относительно
получить и решить стандартное уравнение относительно
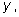 а затем решить уравнение
а затем решить уравнение
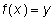 для каждого найденного значения
для каждого найденного значения
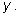 |
|
4. Примеры уравнений, степень которых можно
понизить заменой неизвестного.
1. Биквадратное уравнение.
Это уравнение четвертой степени, содержащее только четные степени
неизвестного:
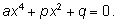 Заменой
Заменой
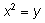 оно сводится к квадратному уравнению.
оно сводится к квадратному уравнению.
Обобщенные биквадратные уравнения сводятся к виду
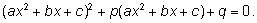
2. Возвратное уравнение.
Это уравнение четвертой степени с симметричными коэффициентами:
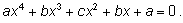
Делением на
х2
и заменой
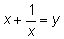 оно сводится к квадратному уравнению.
оно сводится к квадратному уравнению.
Обобщенные возвратные уравнения приводятся к виду
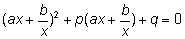
3. Однородные уравнения.
Это уравнения, которые можно привести к виду
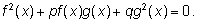 Если
f(x) и
g(x) не
имеют общих корней, то делением на
g2(x)
уравнение приводится к виду
Если
f(x) и
g(x) не
имеют общих корней, то делением на
g2(x)
уравнение приводится к виду
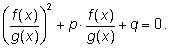
|
| |