| Системы уравнений появляются при решении задач, в
которых неизвестными являются несколько величин. Эти величины
связаны определенными зависимостями, которые записываются в виде
уравнений. |
|
Про набор значений переменных говорят, что он
удовлетворяет данной системе уравнений, если все
уравнения превращаются в тождества при замене переменных этими
значениями. Упорядоченные наборы чисел, удовлетворяющие
системе уравнений, называются решениями системы. |
| Решением также называют сам процесс поиска решений.
Термин «решить систему» означает найти все
решения системы. |
|
Если система имеет хотя бы одно решение, она
называется совместной. Если решений у системы нет, она
называется несовместной. |
|
Слово «несовместность» наглядно показывает, что
уравнения системы накладывают несовместимые друг с другом условия,
которым должны удовлетворять неизвестные. Например, система
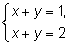несовместна, потому что сумма чисел
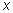и
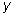не может одновременно равняться
1 и
2.
|
|
Системы называются эквивалентными,
если они имеют одно и то же множество решений. |
Есть множество приёмов, позволяющих перейти от одной
системе к другой, ей эквивалентной (например, добавить к одному
уравнению другое, умноженное на константу). Такими приёмами, как
правило, и осуществляется поиск решения.
В то же время, иногда полезно перейти от одной системы к другой,
множество решений которой включает, кроме решений данной, и другие
наборы (это может произойти, например, при добавлении к одному
уравнению другого, умноженного на переменную). В этом случае, после
окончания процесса решения нужно сделать проверку. |
|
Выберите ровно три из шести возможных параметров (поставив
"галочку"), укажите их значения в соседних полях и нажмите кнопку
"Выполнить".
Автор скрипта Stephen R. Schmitt.
Скрипт разрешён к
модификации и свободному распрстранению.
|
|
Упражнение.
Используя калькулятор "решения треугольника",
выполните следующие задания.
1. Напишите систему из четырёх уравнений,
связывающие переменные
a, b, c, A, B,
C, S.
2. Выберите значения
a, b, c
так, чтобы система
была несовместной (имела одно решение) и проверьте.
3. При задании каких 3 параметров из 6
возможных система будет иметь два решения. Найдите все возможные
случаи. Дайте геометрическое объяснение. |
| |
