Изображение на весь экран - нажать клавишу F11
 
Линейные системы
 
1. Система двух линейных уравнений
Рассмотрим систему


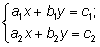
Исследование системы:

1) Если коэффициенты при неизвестных не пропорциональны, т.е. 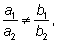   или 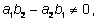   то система имеет единственное решение


2) Если коэффициенты при неизвестных пропорциональны, но они не пропорциональны свободным членам, т.е. 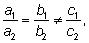   то система решения не имеет.

3) Если коэффициенты при неизвестных и свободные члены пропорциональны, т.е. 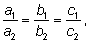   то система имеет бесконечно много решений.
 

2. Геометрическая интерпретация исследования линейно системы
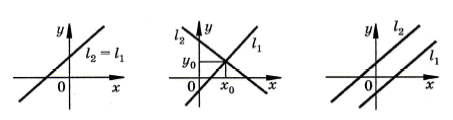
Каждое уравнение линейной системы с двумя неизвестными задает прямую на плоскости. Исследование системы сводится к исследованию расположения двух прямых (прямые могут пересекаться, быть параллельными или совпадать).

 

3. Пример системы трех уравнений с тремя неизвестными
В приложениях встречаются системы линейных уравнений с большим количеством неизвестных. Для их решения в основном используют метод подстановки, которым в принципе можно решить любую такую систему.
Рассмотрим систему трех линейных уравнений с тремя неизвестными:


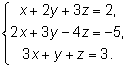
Будем решать систему методом исключения неизвестных. Чтобы исключить  х  из второго и третьего уравнений, надо вычесть из них первое, умноженное соответственно на  2  и на  3.
Получим систему


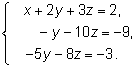
Удобно умножить второе и третье уравнения на  –1,  а затем из третьего уравнения вычесть второе, умноженное на  5.
Получим «треугольную» систему 


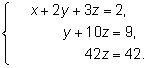
Из последнего уравнения находим 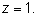   Подставляя в предыдущее уравнение, находим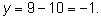 
Подставляя 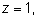 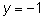    в первое уравнение, получим, 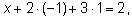   откуда  
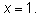
Ответ:    
 

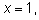
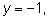
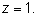
Показанный на этом примере способ решения линейной системы называется методом Гаусса по имени великого немецкого математика, жившего в первой половине XIX в. Метод Гаусса с различными модификациями используется для решения линейных систем с помощью вычислительной техники.
 
  
          Исходная система                                   Текущая система
x +  y +  z =           x +  y +  z = 
x +  y +  z =           x +  y +  z = 
x +  y +  z =           x +  y +  z = 
   

   система введена верно ? 

                                               Возможные действия
                                            -ю  строку разделить на  
 из -й строки вычесть -ю строку, умноженную на

 

Упражнение. Используя манипулятор для метода Гаусса, решите предыдущую систему равнений описанным методом.  Обратите внимание, что после сведения системы к "треугольной" можно вместо подстановки свести систему к "диагональной", выполняя аналогичные операции от последнего уравнения к первому.
 
<< назад               вперед >>
В оглавление модулей / В расписание уроков