|
Прочитайте цитату,
взятую из книги
Д. В. Аносова "Взгляд на математику и нечто из нее"
(текст данной брошюры, вышедшей в серии "Библиотека
"Математическое просвещение" и находящейся в
свободном доступе, представляет собой обработку
записи лекции, прочитанной лауреатом Государственной
премии СССР академиком РАН Д.В. Аносовым 5 декабря 1999
г. для участников III Международного математического
турнира старшеклассников "Кубок памяти А.Н. Колмогорова"
– школьников 8–11 классов). |
|
Цитата.
"Хассе полагал, что древним
грекам однозначность разложения на простые множители
всё-таки была известна. Иное мнение высказано в учебнике
по теории чисел, написанном другим выдающимся учёным –
английским математиком Г. Харди –
совместно с его соотечественником Э.
Райтом. Они указывают, что древнегреческий математик
попросту был бы не в состоянии сформулировать теорему об
однозначности разложения натурального числа на простые
множители, потому что у него не было алгебраических
обозначений. Ведь если я говорю, что "разложение на
простые сомножители единственно", то это не полная
формулировка, а скорее сокращённое название результата.
А в чём же, собственно, он состоит?
Вот в чём. Пусть в дополнение к
разложению
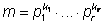 имеется
ещё одно разложение m
на простые множители:
имеется
ещё одно разложение m
на простые множители:
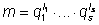 (qi
– простые,
qi
(qi
– простые,
qi 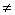 qj
при
i
qj
при
i
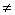 j,
li
– натуральные). Тогда
r
= s, числа
p1,
..., pr с
точностью до порядка, в котором они пронумерованы,
совпадают с q1,
..., qs и
показатели при совпадающих простых сомножителях тоже
совпадают: если pi
= qj,
то
ki
= lj. Попробуйте
сформулировать (только сформулировать!) всё это, не
прибегая к буквенным обозначениям! j,
li
– натуральные). Тогда
r
= s, числа
p1,
..., pr с
точностью до порядка, в котором они пронумерованы,
совпадают с q1,
..., qs и
показатели при совпадающих простых сомножителях тоже
совпадают: если pi
= qj,
то
ki
= lj. Попробуйте
сформулировать (только сформулировать!) всё это, не
прибегая к буквенным обозначениям!
А у Евклида, как указывают Харди и Райт, не было даже
слова для обозначения произведения четырёх и более
множителей". |
|
1) Попробуйте
сформулировать основную теорему арифметики, не прибегая
к современным обозначениям.
2) Попробуйте найти в
сети Интернет обоснования мнения Хассе о том, что
древним грекам однозначность разложения на множители
была известна.
3) В качестве третьего задания приведём
ещё одну цитату из цитированного выше доклада Д.В.
Аносова:
"Вы, вероятно, знаете доказательство иррациональности
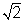 .
А вот используя однозначность разложения на простые
множители, ничего не стоит доказать в два слова, что
если натуральное число
m не является
k-й
степенью никакого натурального числа, то .
А вот используя однозначность разложения на простые
множители, ничего не стоит доказать в два слова, что
если натуральное число
m не является
k-й
степенью никакого натурального числа, то
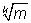 – иррациональное
число. Попробуйте сделать это! Вы увидите, насколько
расширятся ваши возможности при использовании теоремы об
однозначности разложения на простые множители
–
теоремы, упоминание о которой может показаться занудным
педантизмом".
– иррациональное
число. Попробуйте сделать это! Вы увидите, насколько
расширятся ваши возможности при использовании теоремы об
однозначности разложения на простые множители
–
теоремы, упоминание о которой может показаться занудным
педантизмом". |