Цитата.
"Я хочу ещё немного остановиться на различии между числами и будильниками. Что различия имеются, это понятно даже людям, которые от математики далеки: им кажется, что математические объекты скорее напоминают снотворное. Но то различие между математическими объектами и будильниками, о котором я сейчас скажу, может показаться неожиданным. Рассмотрим пародию на арифметику, в которой "ареной действия" является множество  M  натуральных чисел вида  4k+1  с целыми  k 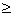0.  Других чисел, кроме таких, для нас сейчас как бы не существует. Множество  M,  как говорят, замкнуто относительно умножения – это значит, что произведение любых двух его элементов снова принадлежит M. Действительно, сразу проверяется, что произведение двух чисел вида  4k+1  снова имеет вид  4k+1.  Некоторые числа из  M  являются произведениями чисел из  M,  ни одно из которых не является единицей.

Другие числа нельзя представить в таком виде; их естественно называть неразложимыми. Почти сразу же очевидно, что  9  – неразложимое число.
(В  M  имеется всего одно число, отличное от  1,  которое меньше  9,  – это  5.  Но  9  не делится на  5).  

Проверим, что  49  тоже неразложимое число. В противном случае мы имели бы
49 = (4a+1)(4b+1) = 16ab+4(a+b)+1
с некоторыми натуральными a, b; отсюда
48 = 16ab+4(a+b),  12 = 4ab+(a+b)>4ab,  3>ab,
что возможно, лишь когда оба натуральных числа a, b равны 1 или когда одно из них равно 1, другое равно 2. Соответствующие произведения были бы  55  или  59;  ни в том, ни в другом случае не получается  49.  
Аналогично доказывается неразложимость  21.  

С другой стороны, каждое разложимое число из  M  разлагается в произведение неразложимых чисел (последние, таким образом, играют в нашей пародийной "системе чисел"  M  такую же роль, какую играют простые числа среди всех натуральных чисел). Действительно, если  m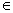M  – разложимое число, то m=kl с некоторыми  k, l 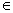M,  причём  k<m,  l<m.  Если оба числа  k, l  неразложимы, то  m  уже представлено в требуемом виде; если одно из них или они оба разложимы, то разложим его (их) на множители, и т. д. При этом рассматриваемые числа всё время уменьшаются, так что рано или поздно этот процесс должен остановиться и мы получим разложение  m  на неразложимые множители. Это рассуждение – точно такое же, каким доказывается, что любое составное натуральное число разлагается в произведение простых чисел; в этом отношении наша пародийная арифметика не отличается от обычной.

А вот в каком она отличается:
441 = 21² = 949, 
причём  21,  9  и  49  – неразложимые элементы  M.  
Выходит, что "будильник"  441  можно разобрать на два одинаковых "колёсика"  21,  а можно – на другие "колёсики"  9  и  49".
 

1) Приведите другие примеры разложимых и неразложимых чисел вида  4k+1   (число "разборных" и "неразборных" "будильников"). Существуют ли разложимые числа вида  4k+1,  имеющие единственное разложение?

2) По аналогии с доказательством бесконечности простых чисел докажите, что число неразложимых чисел вида  4k+1   (число "неразборных будильников") бесконечно.

3) Исследуйте другие множества подобного вида, например,  3k+1.