| В теме "Сравнения"
были приведены примеры таблиц умножения и сложения в
арифметике сравнений. Видно, что первая из них даёт
латинский квадрат
5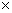 5,
а вторая – латинский квадрат
4 5,
а вторая – латинский квадрат
4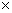 4
(если отбросить нулевые строку и столбец). 4
(если отбросить нулевые строку и столбец).
Таким образом, первая таблица
задаёт латинский квадрат
m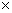 m
формулой
f(n;k) = n+k mod m,
где
n и
k меняются от
0 до
m-1 и обозначают номера строк и столбцов
соответственно (нумерация начинается с нуля). m
формулой
f(n;k) = n+k mod m,
где
n и
k меняются от
0 до
m-1 и обозначают номера строк и столбцов
соответственно (нумерация начинается с нуля). |
|
Вторая таблица задаёт
латинский квадрат
(p-1)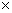 (p-1)
формулой
f(n;k) = n (p-1)
формулой
f(n;k) = n k
mod p,
где
n и
k меняются от
1 до
p-1 и обозначают
номера строк и столбцов соответственно (нумерация
начинается с единицы), а
p –
простое число. k
mod p,
где
n и
k меняются от
1 до
p-1 и обозначают
номера строк и столбцов соответственно (нумерация
начинается с единицы), а
p –
простое число.
Используя арифметику сравнений, можно
построить новые латинские квадраты и написать алгоритмы
их построения (формулы), которые можно впоследствии
запрограммировать и превратить в демонстрационные
программы. |
|
Задания.
1)
Исследовать формулу для построения латинских квадратов
вида
m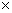 m
формулой
f(n;k) = n+k+c mod m,
где
n и
k меняются от
0 до
m-1 и обозначают номера строк и столбцов
соответственно (нумерация начинается с нуля), а
c –
параметр, который можно менять от
0 до
m-1. Построить все латинские квадраты
размера
4 m
формулой
f(n;k) = n+k+c mod m,
где
n и
k меняются от
0 до
m-1 и обозначают номера строк и столбцов
соответственно (нумерация начинается с нуля), а
c –
параметр, который можно менять от
0 до
m-1. Построить все латинские квадраты
размера
4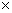 4,
задаваемые этой формулой. 4,
задаваемые этой формулой.
2)
Исследовать формулу для построения латинских квадратов
вида
(p-1)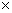 (p-1)
формулой
f(n;k) = c (p-1)
формулой
f(n;k) = c n n k
mod p,
где
n и
k меняются от
1 до
p-1 и обозначают
номера строк и столбцов соответственно (нумерация
начинается с единицы),
p –
простое число, а
c –
параметр, который можно менять от
1
до
p-1. Построить все
латинские квадраты
размера 4 k
mod p,
где
n и
k меняются от
1 до
p-1 и обозначают
номера строк и столбцов соответственно (нумерация
начинается с единицы),
p –
простое число, а
c –
параметр, который можно менять от
1
до
p-1. Построить все
латинские квадраты
размера 4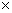 4,
задаваемые этой формулой. 4,
задаваемые этой формулой.
3) При
перестановке столбцов или строк латинского квадрата
получается снова латинский квадрат.
Сколькими способами можно переставить столбцы и строки
латинского квадрата
4 4? 4?
Сколько различных латинских квадратов при этом
получится?
4)* Заметим,
что формулы
n+c1 mod m
и
k+c2 mod m
задают перестановки строк и столбцов, если
n и
k меняются от
0 до
m-1 и обозначают номера строк и столбцов
соответственно,
c1 и
c2
– параметры,
которые и определяют некоторые перестановки (параметры
можно менять от
0 до
m-1).
Постройте все перестановки столбцов и строк, задаваемых
этими формулами и найдите соответствующие этим
перестановкам латинские квадраты.
Сколько их получилось? Сколько из них различных?
Напишите формулы этих квадратов, выразив их через
c1 и
c2
и дайте обоснование количеству различных
латинских квадратов, получаемых такими перестановками.
5)* Заметим,
что формулы
n c1
mod p и
n c1
mod p и
n c2
mod p задают
перестановки строк и столбцов, если
n и
k меняются от
1 до
p-1
и обозначают номера строк и столбцов соответственно,
p
– простое число, а
c1 и
c2
– параметры,
которые и определяют некоторые перестановки (параметры
можно менять от
1 до
p-1). c2
mod p задают
перестановки строк и столбцов, если
n и
k меняются от
1 до
p-1
и обозначают номера строк и столбцов соответственно,
p
– простое число, а
c1 и
c2
– параметры,
которые и определяют некоторые перестановки (параметры
можно менять от
1 до
p-1).
Постройте все перестановки столбцов и строк, задаваемых
этими формулами и найдите соответствующие этим
перестановкам латинские квадраты.
Сколько их получилось? Сколько из них различных?
Напишите формулы этих квадратов, выразив их через
c1 и
c2
и дайте обоснование количеству различных
латинских квадратов, получаемых такими перестановками. |
|
Задание на межпредметные связи с
информатикой.
Используя написанные выше формулы,
написать Java-скрипт,
генерирующий латинские квадраты.
Для знакомства с языком JavaScript
читайте
учебник автора известного самоучителя по этому языку
Дмитриевой Марии Валерьевны, расположенный в
свободном доступе на сайте кафедры информатики
математико-механического факультета Санкт-Петербургского
государственного университета. |