Изображение на весь экран - нажать клавишу F11
 

* ЗАДАНИЕ НА ИССЛЕДОВАНИЕ КЛАССА ФУНКЦИЙ
 
Постановка проблемы. В разделе "Свойства функций" выделены различные характеристики функций и их графиков: нули, промежутки знакопостоянства, экстремумы, промежутки монотонности и пр.  Эти свойства как-то связаны между собой. 

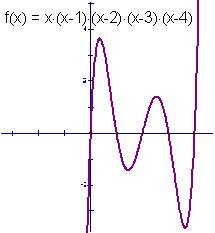
Пример.  На рисунке показана функция. Между каждыми её соседними корнями находится экстремум функции. Таким образом, у функций подобного вида число экстремумов на 1 меньше числа корней. Представляет интерес выяснить, при каких условиях найденная зависимость будет иметь место.
 


 

Цель работы. Исследовать класс функций, свойства которых можно описать следующими утверждениями:

  1. Функции задаются на отрезке и являются непрерывными. Графически непрерывность означает, что график функции можно "нарисовать, не отрывая руки". Точное определение непрерывности смотри здесь.

  2. Для описания промежутков знакопостоянства рассматриваемых функций достаточно следующих утверждений:
    • SP0 – «функция не имеет промежутков положительности»,
    • SP1 – «функция имеет один промежуток положительности»,
    • SN0 – «функция не имеет промежутков отрицательности»,
    • SN1 – «функция имеет один промежуток отрицательности».
  3. Для описания множества корней рассматриваемых функций достаточно следующих утверждений:
    • Z0 – корней нет,
    • Z1 – функция имеет один корень,
    • Z2 – функция имеет два корня,
    • Z3 – функция имеет три корня.
  4. Для описания промежутков монотонности рассматриваемых функций достаточно следующих утверждений:
    • MI0 – «функция не имеет промежутков возрастания»,
    • MI1 – «функция имеет один промежуток возрастания»,
      MI2 – «функция имеет один промежуток возрастания»,
    • MD0 – «функция не имеет промежутков убывания»,
    • MD1 – «функция имеет один промежуток убывания»,
    • MD2 – «функция имеет один промежуток убывания». 
  5. Для описания множества экстремумов рассматриваемых функций достаточно следующих утверждений:
    • Xmin0 – функция не имеет точек минимума,
    • Xmin1 – функция имеет один минимум,
    • Xmax0 – функция не имеет точек максимума,
    • Xmax1 – функция имеет один максимум.
Задания. Найдите как можно больше соотношений между параметрами функций заданного класса. Каждое найденное Вами соотношение можно рассматривать как теорему о непрерывных функциях из этого класса.

Используйте следующие направления исследований.

  1. Изучите связь между утверждениями групп SP (число промежутков положительности), SN (число промежутков отрицательности) и Z (число корней функции).

 
Пример. Можно сформулировать такую теорему: «Если Z0 то либо SP1, либо SN1».
 
  1. Сформулируйте это утверждение, подставив вместо букв обозначаемые ими утверждения.
  2. Попробуйте обосновать корректность этого утверждения и объяснить роль непрерывности в этом доказательстве. Для этого приведите пример разрывной функции, не подчиняющейся теореме.
 
Пример. «Если SP1 и SN1, то либо Z1, либо Z2, либо Z3» (напомним, что функций с большим количеством корней в рамках данной работы мы не рассматриваем).
 
  1. Сформулируйте это утверждение, подставив вместо букв обозначаемые ими утверждения и обоснуйте его корректность.
  2. Приведите примеры, показывающие, что теорема «Если SP1 и SN1, то Z1» неверна.
  3. Изучите связь между утверждениями групп MI, MD (число промежутков монотонности возрастания и убывания) и X (число экстремумов – минимумов или максимумов).
  4. Изучите связь между утверждениями групп Z (число нулей функции) и X (число экстремумов – минимумов или максимумов).
  5. Предложите свои направления для исследований.
Работы учеников.
<< назад               вперед >>
В оглавление / В расписание уроков