| Цель работы. Применение функций показательного и логарифмического роста для оценки сложности задач в дискретной математике. |
|
Пример.
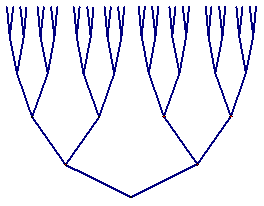
В дискретной математике большую роль играют так называемые бинарные деревья. В каждом узле (узлами или вершинами дерева называют точки, которые соединяются отрезками, называемыми ребрами дерева) сходятся не более трех ребер («веток» дерева). Листом дерева называют узел, в который входит ровно одно ребро. На нашем рисунке все листья находятся наверху. В деревьях часто удобно выделять одну из вершин, которую называют корнем. На нашем рисунке корнем является самый нижний узел. Высотой дерева можно назвать максимальное число ребер в цепочке, соединяющей корень с листом (это число иногда называют расстоянием от корня до вершины). В нашем случае расстояния от корня до всех вершин равны 5. Нетрудно видеть, что наше дерево обладает замечательной симметрией, что позволяет связать высоту дерева H и число его листьев L простой формулой: L=2H.
|
|
Задания.
|
- Cформулируйте алгоритм построения дерева на рисунке.
- Сколько будет листьев у дерева, если нарастить его по этому алгоритму на один уровень?
- Определите зависимость числа всех вершин V
такого дерева от высоты дерева H.
- Определите зависимость высоты дерева H от числа листьев L.
- Определите зависимость высоты дерева H
от числа его вершин V.
- * Найдите в сети Интернет определение идеально сбалансированного дерева и теорему об оценке числа его листьев в зависимости от его высоты; сформулируйте и докажите эту теорему.
- ** Найдите в сети Интернет определение АВЛ сбалансированного дерева и теорему об оценке числа его листьев в зависимости от его высоты; сформулируйте и докажите эту теорему.
- Обязательно приведите ссылку на источник, откуда была взята информация.
|
| Работы учеников. |