Цели работы. В учебнике приведено
определение синуса и косинуса числа:
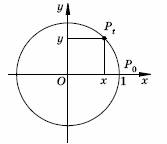
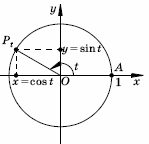
"Синусом числа
t называется ордината
точки, полученной поворотом точки
(1; 0) на угол
t, косинусом числа t
называется абсцисса этой точки".
Это определение связано с движением точки по окружности. Что будет,
если вместо окружности выбрать другую кривую, например гиперболу, а
синус и косинус определять по-прежнему, как ординату и абсциссу
точки? Как выбрать t
таким, чтобы свойства вновь
определенных синуса и косинуса были похожи на свойства обычных
синуса и косинуса. Какие это свойства? |
| |
|
|
| Задания. Найдите в сети Интернет или в
научно-популярных книгах по математике определение гиперболических
функций и исследуйте их свойства. Постарайтесь найти ответы на
следующие вопросы, не забывая указывать ссылки на источники, из
которых черпалась информация. Для ответа используйте
следующую схему: |
|
1. Дайте определение гиперболических функций:
синуса, косинуса, тангенса и котангенса.
2. В чем состоит геометрический смысл параметра
t ?
3. Постройте графики гиперболических функций.
4. Сформулируйте как можно больше свойств гиперболических функций
(чётность-нечетность, периодичность и пр.).
5. Найдите формулы, связывающие значения функций (связь синуса и
косинуса, формулы двойного угла и пр.). Дайте доказательство этих
формул.
6. Проведите сравнительный анализ свойств гиперболических и
тригонометрических функций.
*7. Есть ли, кроме гиперболических и тригонометрических, другие
"синусы" и "косинусы"? |
Замечание. При ответе на вопросы не обязательно
стараться охватить все из них. То же можно сказать про ответы на
вопросы: например, в пункте 4 достаточно найти одно свойство и дать
ему обоснование, а в пункте 5 можно обойтись одной формулой. Дайте
возможность Вашим сокурсникам проявить свои знания!
В то же время, хотелось бы, чтобы все ответы в совокупности давали
достаточно полные ответы на поставленные вопросы. |
| Работы учеников. |