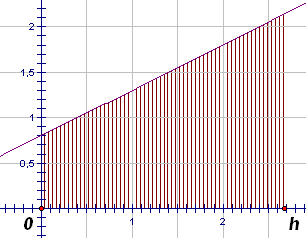
|
Мы знаем, что площадь трапеции равна произведению
полусуммы оснований на высоту. Отсюда получается простая формула
вычисления интеграла (слева на рисунке), которая называется формулой
трапеций. По этой формуле можно точно вычислить интеграл от любой
линейной функции.
Однако для вычисления площади криволинейной
трапеции эта формула обычно будет давать только приближённый
результат (например, если её применить к функции на рисунке справа). |
 |
 |
|
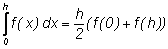
Формула
трапеций |
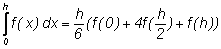
Формула
Симпсона |
|
| Задания 1 |
|
1) Для заданной кубической функции (например,
y=x3-3x2+3x)
найдите промежутки, для которых формула трапеций даёт
точный результат. Объясните причину.
2) Может ли формула трапеций дать точный результат
для обычной параболы, целиком лежащей в положительной полуплоскости?
Объясните причину. |
|
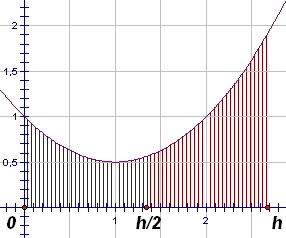
Вместо формулы трапеций можно применить формулу,
которая будет точной не только для линейных функций, но и для
парабол, и не только квадратичных, но даже кубических! Эта формула
(на рисунке справа) называется формулой Симпсона. |
| Задания 2 |
|
1) Вычислите по формуле
Симпсона интеграл
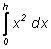и проверьте ответ применением формулы
Ньютона-Лейбница;
2) Вычислите по формуле Симпсона интеграл
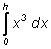и
проверьте ответ применением формулы Ньютона-Лейбница;
3) Вычислите по формуле Симпсона интеграл от
функции, показанной на рисунке ниже, и проверьте ответ применением
формулы Ньютона-Лейбница;
|
| |
 |
|
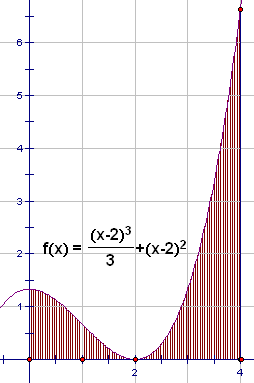Формулу Симпсона можно применить для вычисления
объёмов тел. Например, вычислим объём прямого кругового конуса
с высотой
H и радиусом основания
R, считая S=f(x)
площадью сечения, параллельного основанию и
проведенного на высоте h=x
от основания.
Тогда S(0)=πR2,
S(h/2)=π(R/2)2,
S(H)=0.
По формуле Симпсона результат будет:
H/6(πR2+4π(R/2)2+0)=1/3(πR2H),
что, как мы знаем, является правильной формулой
объёма конуса.
Задания 3 |
|
1) Найдите объём усечённого конуса по формуле
Симпсона.
2) Найдите по формуле Симпсона объёмы шара, шаровой
"шапочки", шарового пояса. |
| Задания 4* |
|
1) Докажите точность формулы Симпсона для интеграла
от любого квадратного трёхчлена
y=ax2+bx+c.
2) Докажите точность
формулы Симпсона для интеграла от любого кубического многочлена
y=ax3+bx2+cx+d.
3) Запишите формулу
Симпсона для интеграла по любому промежутку
[a; b]. |
| |