|
Слово угол употребляется в разных смыслах. |
|
Геометрический угол – это часть плоскости,
ограниченная двумя лучами, выходящими из одной точки – вершины угла. |
|
Когда мы говорим «острый угол», «прямой угол»,
«развернутый угол», «смежные углы», «углы треугольника» и т. п., мы
имеем в виду геометрические углы и связываем с этими понятиями простые
наглядные образы. |
 |
|
Геометрические углы можно сравнивать. Равенство углов определяется
так, как вообще определяется равенство геометрических фигур, т. е. с
помощью движения.
Угол можно делить на равные части. Так биссектриса угла делит его (по
определению) пополам. Одна из знаменитых задач древности – задача о
трисекции угла, которая состоит в том, как с помощью циркуля и линейки
разделить данный угол на три равные части. Нетрудно описать
геометрически, что означает, что один угол меньше или больше другого.
Утверждение «В треугольнике против большей стороны лежит больший угол»
мы легко представляем себе геометрически.
Для сравнения углов их измеряют. Как измеряют углы?
Градусная мера угла
В качестве единицы измерения геометрических углов принят градус
–
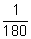 часть развернутого угла. Многие оптические приборы также
используют градусную меру угла. Градусная мера угла позволяет перейти
от геометрических образов к описанию углов с помощью чисел. Так,
прямой угол – это угол в
часть развернутого угла. Многие оптические приборы также
используют градусную меру угла. Градусная мера угла позволяет перейти
от геометрических образов к описанию углов с помощью чисел. Так,
прямой угол – это угол в
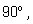 тупой угол – это угол, больший
тупой угол – это угол, больший
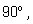 но меньший
но меньший
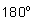 и т. п. Когда мы говорим «сумма углов треугольника равна
и т. п. Когда мы говорим «сумма углов треугольника равна
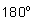 », мы уже под углом понимаем его градусную меру.
Последнему утверждению легко придать чисто геометрический смысл,
построив сумму углов и показав, что она равна развернутому углу.
Аналогично поступить уже с пятиугольником не так просто – утверждение
о том, что сумма его углов равна
», мы уже под углом понимаем его градусную меру.
Последнему утверждению легко придать чисто геометрический смысл,
построив сумму углов и показав, что она равна развернутому углу.
Аналогично поступить уже с пятиугольником не так просто – утверждение
о том, что сумма его углов равна
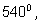 не имеет прежнего геометрического смысла, так как нет геометрического
угла с градусной мерой в
не имеет прежнего геометрического смысла, так как нет геометрического
угла с градусной мерой в
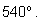
Обобщение понятия угла можно сделать, рассматривая вращательное
движение.
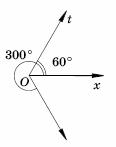
Возьмем два луча, исходящие из одной точки
О. Один луч будем считать неподвижным, а другой
будем вращать вокруг точки
О. На плоскости есть два направления вращения,
которым мы придадим противоположные знаки. Мы привыкли различать
направления вращения стрелок обычных часов, и поэтому направление
любого вращения можно сравнивать с направлением хода часовых стрелок.
По традиции вращение против хода часовых стрелок
считается положительным, а противоположное ему – отрицательным.
|
|
|
|
Обозначим
неподвижный луч через
Ox, а подвижный через
Ot. Если мы остановим подвижный луч, то два луча
разобьют плоскость на два геометрических угла. Обозначим неподвижный
луч через
Ox, а подвижный через
Ot. Если мы остановим подвижный луч, то два луча
разобьют плоскость на два геометрических угла. Одно и то же разбиение,
один и тот же рисунок мы можем получить с помощью различных поворотов.
Так как нас больше интересуют сами повороты, то мы можем обобщить
понятие угла, рассматривая «углы поворота» как некоторую
характеристику вращательного движения.
Понятно, что нужно назвать углом поворота на один
градус – надо вращать подвижный луч от неподвижного в положительном
направлении до тех пор, пока он впервые не займет положение,
образующее с неподвижным лучом геометрический угол в
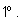
Теперь с помощью этого «единичного поворота» мы сможем определить угол
поворота на любое число градусов. Это число может быть положительным
или отрицательным – различать соответствующие углы поворота мы будем
по направлению вращения. После поворота на
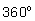 подвижный луч совместится с неподвижным, но мы можем продолжать
вращение и считать, что можно рассматривать углы поворота на
k градусов, где число
k – любое действительное число.
подвижный луч совместится с неподвижным, но мы можем продолжать
вращение и считать, что можно рассматривать углы поворота на
k градусов, где число
k – любое действительное число.
|
|
Пример.
Если зубчатое колесо имеет
72 зубца, то при повороте колеса на
30 зубцов угол поворота будет равен
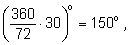 а при повороте на
300 зубцов угол будет равен
а при повороте на
300 зубцов угол будет равен
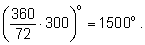 Во втором примере мы видим возникающую на практике необходимость
рассматривать углы повороты, большие
Во втором примере мы видим возникающую на практике необходимость
рассматривать углы повороты, большие
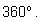
|
| |