|
Углы, получающиеся при непрерывном вращении, удобно
измерять не в градусах, а с помощью таких чисел, которые отражали бы
сам процесс построения угла, т.е. вращение.
Для описания непрерывного вращения градусная мера угла поворота
становится неудобной – с ней трудно связывать другие характеристики
движения, например, скорость или соединять вращательное движение с
иными движениями. Поэтому вводят другую меру угла поворота, так
называемую радианную меру. |
|
|
|
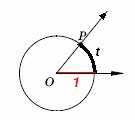
Опишем
окружность радиуса
R с центром в точке
O. Начнем поворачивать подвижный луч и будем следить за
точкой
P пересечения этого луча с окружностью. При вращении
подвижного луча от начального положения, совпадающего с неподвижным
лучом, точка
P будет проходить по окружности некоторый путь, который
можно измерить в тех же единицах длины, что и радиус
R. Отношение пройденного пути к радиусу
R не зависит от радиуса. Если этому отношению еще
приписать знак в зависимости от направления вращения, то мы получим
действительное число
t, которое и называется радианной мерой угла
поворота.
Так как число
t является отношением двух однородных величин
(длин), то оно безразмерно. Поэтому название меры
– 1 радиан
– является в значительной мере условным. Можно
говорить, что угол поворота равен одному радиану, но можно и просто
сказать, что угол поворота равен единице.
Удобно выбрать значение радиуса
R, равное
1. Угол поворота численно будет равен пути, пройденному
точкой
P по единичной окружности, снабженному знаком в
зависимости от направления вращения. |
|
Итак, пусть
t – произвольное действительное число.
Угол
поворота на величину
t (радиан) – это такой угол поворота подвижного
луча, при котором точка пересечения
P этого луча с единичной окружностью пройдет путь равный
| t |,
причём вращение
осуществляется против часовой стрелки при
t > 0 и по часовой стрелке,
если
t < 0. |
|
Развернутый угол измеряется половиной длины единичной окружности. Это
число обозначается буквой
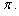 Число
Число
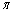 известно людям с глубокой древности и с довольно большой точностью.
Первые десятичные знаки этого числа таковы:
известно людям с глубокой древности и с довольно большой точностью.
Первые десятичные знаки этого числа таковы:
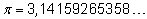
Угол величиной
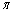 часто используется как самостоятельная мера измерения углов. Прямой
угол равен
часто используется как самостоятельная мера измерения углов. Прямой
угол равен
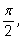 угол в равностороннем треугольнике –
угол в равностороннем треугольнике –
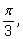 угол, мера которого равна
1 (одному радиану), соответствует некоторому
углу, чуть меньшему, чем
угол, мера которого равна
1 (одному радиану), соответствует некоторому
углу, чуть меньшему, чем
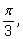 ведь
ведь
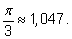
Выведем формулы для перевода из градусной меры в
радианную и обратно. Достаточно сравнить меры для одного и того же
угла, например, прямого:
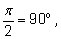 следовательно,
следовательно,
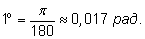
Обратно, можно выразить единицу (т.е. один радиан) в градусной мере:
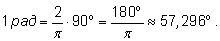
В географии, астрономии и других прикладных науках
используют доли градуса – минуту и секунду. Они обозначаются
соответственно
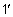 и
и
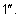 Минута – это
Минута – это
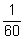 градуса, а секунда –
градуса, а секунда –
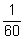 минуты, следовательно,
минуты, следовательно,
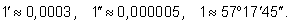
Итак, один и тот же угол можно записать в градусах и радианах. При
этом величину угла в радианах часто можно записать как рациональную
долю угла
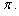 Это можно делать для углов, соизмеримых с развернутым.
Это можно делать для углов, соизмеримых с развернутым.
|
|
Например:
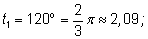
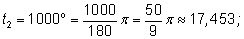
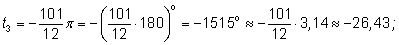
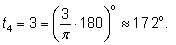
|
| |