|
Один из источников тригонометрических формул – это
изучение поворотов. Поворот точки на угол
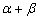 можно представить как композицию двух поворотов – на
угол
можно представить как композицию двух поворотов – на
угол
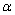 и на угол
и на угол
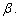
Есть простые формулы, связывающие координаты точек
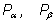 и
и
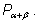 Эти формулы называются формулами сложения.
Эти формулы называются формулами сложения.
Мы выведем формулы, связывающие
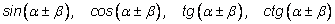 с тригонометрическими функциями углов
с тригонометрическими функциями углов
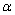 и
и
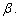 Достаточно вывести формулу косинуса разности,
остальные формулы получатся как ее следствия.
Достаточно вывести формулу косинуса разности,
остальные формулы получатся как ее следствия. |
Косинус разности двух углов равен произведению косинусов этих углов,
сложенному с произведением синусов:
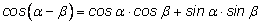
|
 |
|
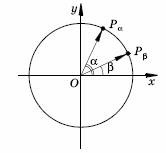
Доказательство.
Построим углы
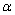 и
и
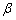 с помощью единичной окружности, т. е. точки с помощью единичной окружности, т. е. точки
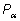 и и
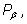 такие, что векторы
такие, что векторы
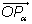 и
и
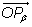 образуют углы
образуют углы
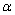 и и
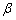 с положительным направлением оси абсцисс. Угол
между векторами
с положительным направлением оси абсцисс. Угол
между векторами
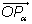 и
и
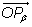 равен
равен
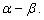 Вычислим
скалярное произведение этих векторов. По определению скалярного
произведения:
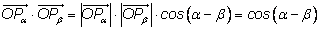 (так как векторы
(так как векторы
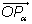 и
и
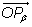 имеют
длину, равную
1).
имеют
длину, равную
1).
Теперь вычислим это же скалярное произведение с помощью координат: 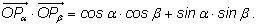
Сравнивая результаты вычислений, получаем требуемую формулу:
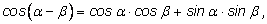 что и требовалось доказать. что и требовалось доказать. Выведем остальные формулы. Косинус суммы.
Сумму
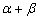 представим как разность представим как разность
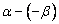 и подставим в формулу для
косинуса разности: и подставим в формулу для
косинуса разности:
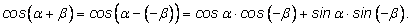
Воспользуемся тем, что
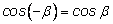 (четность косинуса), а (четность косинуса), а
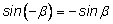 (нечетность синуса). Получим: (нечетность синуса). Получим: |
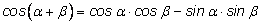
|
|
Синус суммы.
Воспользуемся одной из формул приведения:
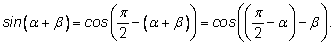 Теперь по формуле косинуса разности получим:
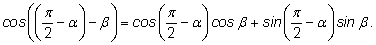 . . Окончательно |
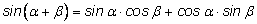
|
|
Синус разности.
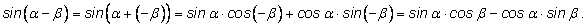 |
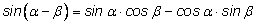
|
|
Тангенс суммы и разности.
По определению
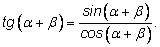 По
формулам синуса и косинуса суммы имеем: По
формулам синуса и косинуса суммы имеем:
 Разделив числитель и знаменатель этой дроби на
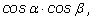 получим: получим: |
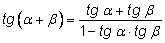
|
|
Заменяя
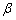 на на
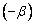 и пользуясь нечетностью тангенса,
получаем: и пользуясь нечетностью тангенса,
получаем: |
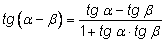
|
| |